|
  neue Homepage neue Homepage
Die Mathematik (μαθηματική τέχνη mathēmatikē téchnē ‚die Kunst des Lernens‘, ‚zum Lernen gehörig‘) ist eine Wissenschaft, welch aus der Untersuchung von geometrischen Figuren und dem Rechnen mit Zahlen entstand.

vom Stoff der ersten Klasse Volksschule bis zum Stoff Maturaniveau ( HTL,HAK,Gymnasium,Glasfachschule, ...etc.)
einige Themen aus dem großen Spektrum der interessanten Mathematik :
- dividieren, multiplizieren, addieren, subtrahieren ( ohne Taschenrechner ! )
- runden von Zahlen
- einfache Textaufgaben (Sachprobleme lösen)
- Wurzelziehen ( ohne Taschenrechner ! )
- Mengenlehre: Durchschnittsmenge, Vereinigungsmenge, Komplementärmenge, Venn-Diagramme (Mengendiagramme)
- Kommutativgesetz (Vertauschungsgesetz), Assoziativgesetz (Verbindungsgesetz), Distributivgesetz (Verteilungsgesetz)
- Rechnen mit Klammern - KLAPUSTRI
Bsp.: Vereinfache: -[ 2x - ( 8 + x) -4x] - (x + 2)² =
- Längenmaße, Flächenmaße, Volumsmaße
- Massenmaße (Gewichtsmaße)
- Zahlenmengen: natürliche Zahlen, ganze Zahlen, rationale Zahlen, irrationale Zahlen, reelle Zahlen
- Rauminhalte verschiedener Körper
 so nicht ! so nicht !
Bruchrechnen: Addition und Subtraktion von Brüchen, multiplizieren, dividieren, gemischte Brüche, unechte Brüche, echte Brüche, uneigentliche Brüche
- Rechnen mit Termen: binomische Formeln, Monome, Binome, Polynome; Multiplizieren von Polynomen, Division eines Polynoms durch ein Monom, Polynom dividiert durch Polynom ...usw.; das Pascal-Dreieck (Koeffizienten), Bruchterme
Beispiele : ( a + 2b)² .... binomische Formel
x², 3a, 4yx, u .... Monome
( x² + 3 ) : x .... Binom dividiert durch Monom
( a +4b +3x ) ( a +b ) .... Polynom mal Binom
( a + b )³ = a³ + 3a²b + 3ab² +b³
- Dreieck, Quadrat, Rechteck,Sechseck: Fläche und Umfang
- Der Würfel und der Quader: Oberfläche, Volumen, Diagonalen, Netz zeichnen
- Prismen : Oberfläche und Volumen
- Deltoid, Parallelogramm und Raute (Rhombus)
- Pyramiden: Oberfläche und Volumen
- Kreis, Kreissektor und Kreissegment
- Tetraeder, Oktaeder
 Ein Tetraeder ist ein Körper aus vier gleichseitigen Dreiecken Ein Tetraeder ist ein Körper aus vier gleichseitigen Dreiecken
- besondere Körper: Parallelepided, schiefe Pyramiden, Kegelstumpf, unregelmäßige Pyramiden
- zusammengesetzte Körper
- Lehrsatz des Pythagoras :
 Pythagoras von Samos (griechisch Πυθαγόρας) (* um 570 v. Chr., † nach 510 v. Chr.) war ein griechischer Philosoph und Gründer einer einflussreichen religiös-philosophischen Bewegung. Pythagoras von Samos (griechisch Πυθαγόρας) (* um 570 v. Chr., † nach 510 v. Chr.) war ein griechischer Philosoph und Gründer einer einflussreichen religiös-philosophischen Bewegung.
- Umformen von Gleichungen 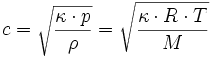 R = ? R = ?
- Mischungsaufgaben
Bsp.:
Wie viel Liter 20%-ige Schwefelsäure muss man mit 50%-iger mischen, um 20 Liter 28%-ige Schwefelsäure zu erhalten ?
Wie viel Liter Wasser muss man zu 70%-igem Alkohol dazumischen, um 10 Liter 25%-igen Alkohol zu erhalten ?
Mischungsaufgaben oder Mischungsgleichungen sind ein Untergruppe mathematischer Problemstellungen, bei denen mehrere Stoffe mit unterschiedlichen Eigenschaften gemischt werden um einen Stoff mit vorherbestimmten, neuen Eigenschaften zu erhalten.
- Leistungsaufgaben, Bewegungsaufgaben :
Die Leistungs- und Bewegungsaufgaben bereiten den Schülern oft große Schwierigkeiten. Die Schwierigkeit besteht darin, den Text in entsprechende Gleichungen umzusetzen.
Bsp. Bewegungsaufgabe :
Ein Güterzug fährt um 08:00 vom Ort A mit v=80 km/h weg. Eine halbe Stunde später fährt ihm ein Schnellzug von B aus in Richtung A mit v=120 km/h entgegen. Die Orte sind 200 km voneinander entfernt. Wann und in welcher Entfernung von A treffen sie sich ? Zu welcher Uhrzeit ist der Güterzug in Sichtweite (200 m) des Schnellzuges ?
Bsp. Leistungsaufgaben :
Ein Tank soll leergepumpt werden. Pumpe 1 würde dazu allein 3 Stunden benötigen, Pumpe2 2 Stunden und Pumpe 3 würde im Alleinbetrieb 2,5 Stunden benötigen. Wie lange dauert das Auspumpen wenn zuerst Pumpe1 läuft, eine halbe Stunde später Pumpe2 und eine weitere halbe Stunde später Pumpe3 dazugeschaltet wird ?
oder :
Eine Hyäne alleine frisst ein Schwein in 3 Stunden auf, ein Tiger alleine frisst das Schwein in 1 Stunde und ein Löwe in einer Dreiviertelstunde. Wie lange dauert es, wenn alle drei zusammen das Schwein auffressen ?
- Gleichungssysteme ( Gleichungen mit 2 oder mehreren Unbekannten ) Eliminationsverfahren nach Gauß, Determinantenmethode, Einsetzungsverfahren...etc.
Bsp.: I) 2x - 3y + z = 8
II) 3x - y - 8z = -1
III) -x - 4y +2z = 3
- Trigonometrie: Sinus, Cosinus, Tangens, Sinussatz, Cosinussatz. Vermessungsaufgaben, Höhensatz, Kathetensätze, Zentriwinkel
Bsp. zu Vermessungsaufgabe:
Von einem 1800 m hohen Berg sieht man die Ortschaft A unter dem Tiefenwinkel 34°. Nach Schwenken des Fernrohrer um den Horizontalwinkel 55° sieht man die Ortschaft B unter dem Tiefenwinkel 48°. Berechnen Sie die Entfernung der beiden Ortschaften.
- Der hypberbolische Sinus
sinh(x) = (e^x - e^(-x))/2 ,
der hyperbolische Cosinus cosh(x) = (e^x + e^(-x))/2; die Umkehrfunktionen dazu heißen hyperbolometrische Funktionen
Anwendung in der Natur: Durchhängekurven ( Seilkurven ) sind cosh-Funktionen !
Seilkurve: x = a*cosh[A/a]
 Durchhang einer Freileitung Durchhang einer Freileitung
- Summensätze der Trigonometrie
- Halbwinkelsatz und Doppelwinkelsatz
- Trigonometrische (goniometrische) Gleichungen
- Rechnen mit Potenzen und Wurzeln
- Grad, Neugrad und Bogenmaß; Raumwinkel : Umrechnen mit dem Taschenrechner ( TI30 )
- quadratische Gleichungen und Ungleichungen : Satz von Vieta
Bsp.: 3x² + 4x - 5 = 0 quadr.Gleichung allgemeine Form
x² + px +q = ( x - x1)(x - x2) Satz von Vieta, Zerlegung in Linearfaktoren
- Bruchgleichungen
- Bruchungleichungen
Relationen: Zeichnerische Darstellung, Menge AxB 
immer wieder ein Lieblingsthema der Schüler der 5. / 6. Klasse Gym: :-(
Vektorrechnung:
Grundlagen: Ortsvektor, Einheitsvektor, Skalarprodukt, vekt.Produkt, Winkel zwischen zwei Vektoren , Betrag eines Vektors, Addition von Vektoren, Append-Regel
Lagebeziehung Gerade-Ebene, Lagebeziehung zweier Ebenen, Lagebeziehung mehrerer Ebenen; Abstand Punkt-Gerade, Normalvektorform der Ebene, Parameterdarstellung der Ebene, parameterfreie Form der Ebene und der Geraden
Darstellung von Ebenen und Geraden: Parameterform, Normalvektorform, allgemeine (=parameterfreie Form), Hauptform; Umwandlung untereinander
Bestimmung des Inkreismittelpunktes, Schwerpunktes, Umkreismittelpunktes und Höhenschnittpunktes eines Dreiecks mittels Vektorrechnung
Abstand Punkt-Ebene, Abstand Punkt-Ebene, hesseschen Normalform
.
Beispiele zur Vektorrechnung :
- Bestimmen Sie die Gleichung der Ebene, die normal auf die Gerade X = ( 1/2/7) + t(-2/-3/9) steht und durch den Punkt Q (4/5/-1) geht
- Berechnen Sie den Inkreismittelpunkt des Dreiecks A (0/1), B (5/2) und C (3/7) mit Hilfe der Vektorrechnung
- Geben Sie eine allgemeine Ebenengleichung der Ebene X = (3/4) + s(-1/-2) + t(5/4) an
- Lagebeziehung Ebene-Ebene: Wie stehen die Ebenen E1: X = (8/2) + s(-1/-2) + t(3/-4) und E2: X = (0/6) + s (1/6) + t(9/11) zueinander ? Geben Sie eine Normalvektorform beider Ebenen an und berechnen Sie die Schnittgerade !
- Spiegeln Sie den Punkt P(3/2/-4) an der Ebene X = (2/3/7) + s(-2/4/8) + t(-5/2/9)
- Berechnen Sie den Umkreismittelpunkt des Dreieckes A(-5/1), B(3/2), C (1/7)
- Schneiden Sie die Gerade X = (2/4/5)+ w(-1/2/5) mit der Ebene X = (1/2/3) + s(-2/-4/-5) + t(7/-8/-1) Wo liegt der Schnittpunkt ?
- Eine Gerade g: X = (2/4/6) + s(-3/5/9) durchstößt eine Ebene orthognonal im Punkt P(8/2/-1) der Ebene. Geben Sie eine Parameterdarstellung der Ebene an !
Geometrie
Die Geometrie ist ein Teilgebiet der Mathematik, das aus der Beschäftigung mit den Eigenschaften und Formen des Raumes sowie der Gestalt ebener und räumlicher Figuren, Berechnungen von Längen, Flächen, Inhalten entstand.

Unterschieden wird in analytische Geometrie (Punkte der Ebene durch Koordinaten festlegen), Planimetrie (ebene Geometrie), Stereometrie (räumliche Geometrie) und Trigonometrie (Berechnung von Längen und Winkeln geometrischer Figuren.
- analytische Geometrie:
Hyperbel, Parabel, Ellipse, 1. und 2.Hauptlage, Kreisgleichung, Tangenten, Berührbedingungen, Spaltform
Bsp.:
Von einer Hyperbel in 1.Hauptlage kennt man den Brennpunkt F(1/0) und einen weiteren Punkt P (3/4); Wie lautet die Gleichung der Hyperbel ? Wie lauten die Gleichungen der Asymptoten ? Legen Sie die Tangente an den Punkt (6/y) der Hyperbel !
Funktionen: lineare Funktion, quadratische Funktion, Nullstellen und
Eigenschaften, Scheitelpunkt der Parabel, quadratische Ergänzung
Schnittpunkte zweier Graphen, Hyperbeln
Beispiele:
a) Eine Gerade g geht durch die Punkte P (2/3) und Q (-1/-6). Die Gerade h ist normal auf g und geht durch den Punkt T(5/7). Berechnen Sie die Funktionsgleichung von g und h ! Welchen Steigungswinkle haben die Geraden ?
b) geg.: quadratische Funktion mit y = 2x² + x -10 Berechnen Sie die Nullstellen und den Scheitelpunkt !
c) Berechnes Sie die Schnittpunkte der Parabel y = 2x² - 1 mit der Geraden y = 0.5x
- Polynomdivision und Partialbruchzerlegung
Bsp. Polynomdivision: (x³ + 2x² -5) : (x - 2) =
Die Partialbruchzerlegung ist eine Möglichkeit, rationale Funktionen in einer einfacheren Form darzustellen, damit wird ihre weitere Barbeitung erleichtert :
1.) Bsp. für Partialbruchzerlegung (einfache Nullstellen) :
 die Konstanten a1 und a2 bestimmt man durch Koeffizientenvergleich; somit ist die Darstellung rechts vom Gleichheitszeichen eine einfachere Darsellung der Ausgangsfunktion. die Konstanten a1 und a2 bestimmt man durch Koeffizientenvergleich; somit ist die Darstellung rechts vom Gleichheitszeichen eine einfachere Darsellung der Ausgangsfunktion.
Die Partialbruchzerlegung wird beim Integrieren, bei der Laplace-Transformation und bei der z-Transformation benötigt.
2.) Beispiel (doppelte Nullstelle) :
 a11, a12 durch Koeffizientenvergleich betimmen a11, a12 durch Koeffizientenvergleich betimmen
. x=1 ist hier die einzige, aber doppelte Nullstelle
- logische Verknüpfungen und Schaltalgebra:
UND-Verknüpfung, ODER-Verknüpfung, Negation, NAND und NOR-Gatter, Wahrheitstabelle, disjunktive Normalform, konjunktive Normalform, Realisierung der Gatter in der Elektronik
Die Schaltalgebra ist eine spezielle Ausprägung der Booleschen Algebra, die auf Schaltanordnungen zugeschnitten ist. Sie dient als Hilfsmittel zur Berechnung binärer Schaltnetze und Schaltwerke. Der Begriff binär bezieht sich in der Schaltalgebra auf die beiden Schalterzustände geöffnet und geschlossen.
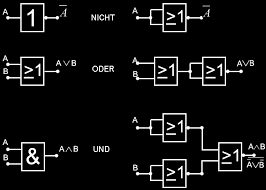
- Kosten- und Preistheorie: Kostenfunktion, Gewinnfunktion, Erlös, Betriebsoptimum, Gewinnschwelle, Betriebsminimum , Preiselastizität
- lineare Optimierung
- lineare Interpolation
- Newtonsche Näherungsverfahren
 Sir Isaac Newton 1643 - 1727 Sir Isaac Newton 1643 - 1727
Sir Isaac Newton war englischer Mathematiker und Physiker. Newton gilt als der Begründer der klassischen theoretischen Physik und damit der exakten Naturwissenschaften. Als einer der bedeutendsten Wissenschaftler der Neuzeit leistete er grundlegende Beiträge in vielen Wissenschaftsgebieten. Seine Entdeckungen und Theorien bildeten den Grundstock für ein naturwissenschaftliches Weltbild, das über zwei Jahrhunderte Gültigkeit hatte.
- Einführung in die Welt der komplexen Zahlen C; Anwendung in der Elektrotechnik : Reihen-und Parallelschaltungen von Widerständen, Spulen und Kondensatoren komplex berechnen
Die Zahl z = a + b.i heißt komplexe Zahl; i nennt man die imaginäre Einheit
Beispiele für komplexe Zahlen: z1 = 3 + 4.i ; z2 = -2,34 + 1,7.i

- Die Exponentialfunktion und der Logarithmus:
Rechenregeln, Anwendungen ( exponentieller Zerfall und exp. Wachstum ) ; Exponentialgleichungen und Logarithmusgleichungen, Beispiele dazu ( Vermehrung von Bakterien, radioaktiver Zerfall )
Bsp. für exp. Wachstum: Die Fläche eines Waldes mit anfangs 20 ha verdoppelt sich alle 30 Jahre.
a) Stellen Sie das Wachstumsgesetz auf b) Wie viel ha hat man nach 100 Jahren ?
b) Nach welcher Zeit hätte man 300 ha ?
Bsp. für exp. Zerfall:
Ein radioaktiver Stoff hat eine Anfangsmasse von 2 kg und eine Halbwertszeit von 400 Jarhen.
a) Stellen Sie das Zerfallsgesetz auf
b) Nach wie viel Jahren hat man nur mehr 1 % der Anfangsmenge ?
- das Summensymbol 
Bsp.: Schreibe mit Hilfe des Summenzeichens
3 + 12 + 48 + . . . Hinweis: Hebe 3 heraus.
- Folgen und Reihen
Konvergenz, arithmetische Folgen und Reihen, geometrische Folgen und Reihen , Grenzwert einer konvergenten geometrischen Reihe, geometrische Beispiele dazu, Monotonie und Schranken von Folgen, Grenzwerte von Folgen und Reihen ( Limes ), Epsilon-Umgebung und Grenzwertsätze
geometrisches Beispiel zu Folgen und Reihen:
Auf einen Würfel mit a=5cm wird ein zweiter Würfel gestellt mit einer um 40% kürzeren Seitenkante; auf diesen wird wieder ein Würfel gestellt, dessen Seitenkante wiederum um 40% kürzer ist ...usw. Berechnen Sie a) Die Summe der ersten 20 Volumina der Würfel b) Die Summe aller (unendlich vielen) Volumina
oder:
An einen Halbkreis mit dem Radius r wird ein halb so großer Halbkreis angefügt, daran wieder ein halb so großer usw., so dass eine Spirale entsteht (Bild). Berechnen Sie die Länge der Spirale ! (unendlich viele Halbkreise)
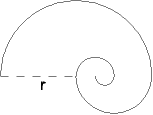
oder:
Drei Zahlen sind aufeinanderfolgende Glieder einer geometrischen Reihe. Ihr Produkt ist 1728, die Summe aus dem zweiten und dritten Glied ist 28. Wie groß ist die Summe der drei Glieder?
- Differenzenquotient und Differentialquotient
- Erklärung des LIMES ; Ableitung mit Hilfe des Limes
 . Schreibweise für den Grenzwert a einer Folge . Schreibweise für den Grenzwert a einer Folge
Eine Folge kann in der Mathematik die Eigenschaft haben, sich mit wachsendem Index immer mehr einer bestimmten Zahl anzunähern. Diese Zahl nennt man Grenzwert oder Limes der Folge. Besitzt eine Folge solch einen Grenzwert, so wird sie konvergent, andernfalls divergent genannt.
- Integralrechnung
Historisches
Flächenberechnungen werden seit der Antike untersucht. Im 5. Jahrhundert vor Christus entwickelte Eudoxos von Knidos nach einer Idee von Antiphon die Exhaustionsmethode, die darin bestand, einen Körper durch regelmäßige Polygone auszufüllen. Er konnte so Flächen als auch Volumina einiger einfacher Körper bestimmen. Archimedes (287–212 v. Chr.) verbesserte diesen Ansatz, und so gelang ihm die exakte Integration einer Parabel, alles ohne Benutzung eines Grenzwertbegriffs.
- Hauptsatz der Differential- und Integralrechnung
 Hauptsatz der Diff.- und Integralrechnung Hauptsatz der Diff.- und Integralrechnung
- Grundintegrale
Anwendung der Integralrechnung : Flächen- und Volumsberechnung ( Rotation um die x-Achse, Rotation um die y-Achse )
Ein Paraboloid entsteht durch Drehung einer Parabel, hier z.Bsp. um die y-Achse
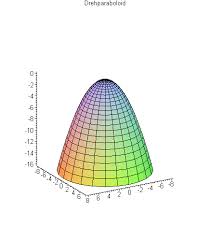
partielle Integration, Integrieren durch Substitution, Integration durch Partialbruchzerlegung, uneigentliche Integrale, numerische Integration, Näherungsverfahren (Kepler, Simpson), Trapezformel, Integration über mehrdimensionale Bereiche
Differentialrechnung
Die Differential- bzw. Differenzialrechnung ist ein Gebiet der Mathematik und ein wesentlicher Bestandteil der Analysis. Sie ist eng verwandt mit der Integralrechnung, mit der sie unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird. Zentrales Thema der Differentialrechnung ist die Berechnung lokaler Veränderungen von Funktionen.
Historisches
Die Aufgabenstellung der Differentialrechnung war als Tangentenproblem seit der Antike bekannt. Der nahe liegende Lösungsansatz war die Approximation der Tangente als Sekante über einem endlichen (endlich heißt hier: größer als null), aber beliebig kleinen Intervall. Die technische Schwierigkeit bestand darin, mit einer solchen infinitesimal kleinen Intervallbreite zu rechnen. So löste Pierre de Fermat um 1640 das Tangentenproblem für Polynome. Hierbei schrieb er bereits eine Ableitung hin, jedoch ohne Betrachtung von Grenzwerten und ohne niederzuschreiben, was die mathematischen Rechtfertigungen für sein Vorgehen waren. Zur selben Zeit wählte Descartes einen algebraischen Zugang, indem er an eine Kurve einen Kreis anlegte. Dieser schneidet die Kurve in zwei Punkten, es sei denn, der Kreis berührt die Kurve. Dann war es ihm für spezielle Kurven möglich, die Steigung der Tangente zu bestimmen.
Ende des 17. Jahrhunderts gelang es Isaac Newton und Gottfried Wilhelm Leibniz unabhängig voneinander, widerspruchsfrei funktionierende Kalküle zu entwickeln . Newton ging das Problem jedoch von einer anderen Seite an als Leibniz.
der Differenzenqotient und Differentialquotient; das Tangentenproblem
Ableiten mit Hilfe des limes ( Delta x gegen 0 )
Ableitungsregeln: Ableitung einer Summe, Ableitung einer Konstanten, Ableitung einer konstanten Funktion, Potenzregel, Quotientenregel, Produktregel, Kettenregel
implizit differenzieren
Anwendung der Differentialrechnung: Kurvendiskussion und Extremwertaufgaben
Wahrscheinlichkeitsrechnung :
Manche Aufgaben können wir uns mit einem Baumdiagramm veranschaulichen (s.u.).
Beispiel:
Eine Urne enthält 3 rote und 6 blaue Kugeln. Es wird 3mal je eine Kugel gezogen.
.........Ziehen geordneter Stichproben mit Zurücklegen und ohne Zurücklegen, Ziehen ungeordneter Stichproben, Baumdiagamme, Wahrscheinlichkeiten...etc.
Würfeln, Lotto, Totto, Ziehen von Kugeln verschiedener Farben aus einem Sack...etc.
Bsp.:
In einem Sack befinden sich 3 rote, 4 weiße und 5 blaue Kugeln Wie groß ist die Wahrscheinlichkeit, dass man hintereinander 1 rote und 1 blaue Kugel zieht ? (ohne zurücklegen)
oder:
In einem Regal stehen 5 CDs von AC/DC, 7 CDs von Iron Maiden und 6 CDs von Metallica. Wie groß ist die Wahrscheinlichkeit, dass man
a) hintereinander eine CD von AC/DC und Metallica zieht ?
b) hintereinander 2 CDs der selben Gruppe zieht ? (ohne zurückstellen der CDs )
Statistik:
absolute Häufigkeit, relative Häufigkeit, Mittelwert, Median, Modus, Varianz, Standardabweichung, Spannweite, Gauß'sche Glockenkurve, Nomalverteilung
Bsp: In einem Kurs befindes sich Personen mit folgendem Alter:
22 23 25 22 26 23 23 25 22 20 21 21 22 24 25 26 22 21 20 23 24 25
Stellen Sie eine Tabelle mit der Häufigkeitsverteilung auf und berechnen Sie die Spannweite, den Mittelwert,die Varianz und die Standardabweichung; Wie groß sind Median und Modus ?
Die Standardabweichung ist ein um 1860 von Francis Galton eingeführter Begriff der Statistik und der Wahrscheinlichkeitsrechnung und ein Maß für die Streuung der Werte einer Zufallsvariablen um ihren Mittelwert. Sie ist für eine Zufallsvariable X definiert als die positive Quadratwurzel aus deren Varianz .
Einführung in die wunderbare Welt der Differentialgleichungen 
- Differentialgleichungen 1.Ordnung
- Differentialgleichungen 2. Ordnung
y' = x + 2y Diff.Gleichung 1.Ordnung
y'' + y' = e^x Diff.Gleichung 2.Ordnung
Technische Anwendungen:
die Diff.Gleichung der freien ungedämpften Schwingung,
die Diff.Gleichung der Drehschwingungen (Pendelbewegung)
Differentialgleichung der gedämpften Schwigung :
 Differentialgleichung der freien gedämpften Schwingung m:Masse R:Reibungskoeffizient D:Federekonstante Differentialgleichung der freien gedämpften Schwingung m:Masse R:Reibungskoeffizient D:Federekonstante
 Tatsächliche physikalische Schwingungen sind immer gedämpft Tatsächliche physikalische Schwingungen sind immer gedämpft
die Differentialgleichung der Knickung (Mechanik),
Entladung eines Kondensators ( als elektrisches Gégenstück zu gedämpften Schwingungen),
Resonanzwirkung ( Mechanik )
weitere Anwendungen der Differential- und Integralrechnung:
Integraltransformationen:
- Taylor-Reihe : Darstellung von Funktionen mit Hilfe von Potenzreihen an einem bestimmten Punkt
Im Spezialfall a = 0 wird die Taylor-Reihe manchmal auch Maclaurin-Reihe genannt.
-
Sei I ein reelles Intervall und  eine beliebig oft differenzierbare Funktion, dann heißt die im Folgenden dargestellte unendliche Reihe die TAYLOR-Reihe von f im Entwicklungspunkt a: eine beliebig oft differenzierbare Funktion, dann heißt die im Folgenden dargestellte unendliche Reihe die TAYLOR-Reihe von f im Entwicklungspunkt a:
 
-
- FOURIER - Transformation : eine Funktion wird einer anderen Funktion ( ihrer Fouriertransformierten) zugeordnet ;
Sie ist eng verbunden mit der Laplace-Transformation:

Laplace-Transformation
- LAPLACE-Transformation : Die Laplace-Transformation bildet reellwertige Originalfunktionen auf komplexwertige Bildfunktionen ab. Die wichtigste Eigenschaft der Laplace-Transformation besteht nun darin, dass der Differentiation und Integration im reellen Originalbereich einfache algebraische Operationen im Bildbereich entsprechen. Bei vielen Anfangs- und Randwertproblemen spielt der Zeitbereich die Rolle des reellen Originalbereiches und der Frequenzbereich oder Spektralbereich diejenige des komplexen Bildbereiches.
 
|



